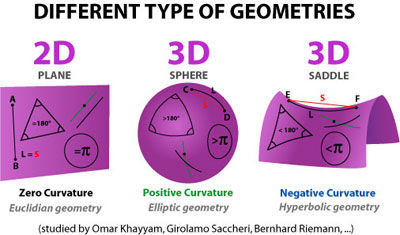
In high school we are taught advanced geometry, and many if not most of us were either bamboozled by it, fascinated by it or extremely scared of it. This kind of geometry is called euclidean geometry. This kind of geometry is only applicable for completely plain surfaces. In euclidean geometry we know that the interior angles of a triangle always add up to 180 degrees and parallel lines always meet. However all these postulates don't hold true in curved space. Now there are three kinds of planes: a zero curvature plane, a positive curvature plane and a negative curvature plane.
A piece of paper is an example of a zero curvature space, A ball's surface is an example of positive curvature and a saddle is an example of negative curvature.
In a zero curvature plane one sees that the angles in a triangle are always equal to 180 degrees, parallel lines never meet, the shortest distance between two points is a straight line and the circumference of a circle is always equal to 2πr (where is r the radius of the circle). In a surface with positive curvature some thing interesting happens. Here, the angles of a triangle always add up to a value greater than 180 degrees, parallel converge at a point, the shortest distance between two points is a curved line known as a geodesic and the circumference is always greater than 2πr. In a surface with negative curvature, just like a positively curved plane, the shortest line between two points is a geodesic and and parallel lines converge at a point. The only difference here is that in negative curvature, the angles of a triangle add up to a sum of less than 180 degrees and that the circumference of a circle is less than 2πr.
Though, the ideal conditions for us might be flat, we like the scientists of yesteryear must learn how to adapt and derive solutions to whatever life may throw at us.
Comments